Covariance
Explained.
Introduction to Covariance
Covarianceis a mathematical term that describes how two variables move together. Positive covariance means they rise and fall together, whereas negative covariance means they move in opposite directions. And if there's no clear pattern? The covariance will be close to zero.
While this may sounds simple, the more data you have, the more complicated it tends to become. When we analyze big data, these relationships are harder and harder to find. Also, not all relationships are equal: some are subtle, some are strong, and we need a way to measure that, too.
While this may sounds simple, the more data you have, the more complicated it tends to become. When we analyze big data, these relationships are harder and harder to find. Also, not all relationships are equal: some are subtle, some are strong, and we need a way to measure that, too.
Positive Covariance
When two variables have positive covariance, it means they tend to increase or decrease together. In other words, when one goes up, the other usually does too — and when one drops, the other tends to follow.
For example, consider ice cream sales and temperature: on hotter days, ice cream sales typically rise. While on cooler days, ice cream sales will lessen. If you plot the data, you’d often see an upward trend — both variables moving in the same direction. Positive covariance helps us identify relationships where things move in tandem.
For example, consider ice cream sales and temperature: on hotter days, ice cream sales typically rise. While on cooler days, ice cream sales will lessen. If you plot the data, you’d often see an upward trend — both variables moving in the same direction. Positive covariance helps us identify relationships where things move in tandem.
Negative Covariance
Negative covariance shows the opposite relationship. When one variable increases, the other decreases — they move in opposite directions.
Imagine the relationship between the number of hours a student spends on social media and their test scores. As time on social media goes up, scores may go down (at least in some studies!). This suggests a negative covariance: an inverse relationship where more of one thing often means less of another.
Imagine the relationship between the number of hours a student spends on social media and their test scores. As time on social media goes up, scores may go down (at least in some studies!). This suggests a negative covariance: an inverse relationship where more of one thing often means less of another.
No Covariance
When there's zero covariance, there’s no consistent pattern in how the two variables move. Sometimes they rise together, sometimes they move in opposite directions — but overall, there’s no predictable trend.
Think of rolling a die and measuring the outdoor temperature at the same time. These two things are unrelated. Zero covariance means there's no measurable connection between the changes in one variable and changes in the other.
Think of rolling a die and measuring the outdoor temperature at the same time. These two things are unrelated. Zero covariance means there's no measurable connection between the changes in one variable and changes in the other.
Covariance Formula
To actually calculate covariance, we use a mathematical formula. The covariance formula looks at how much two variables change together — not just how much they change individually.
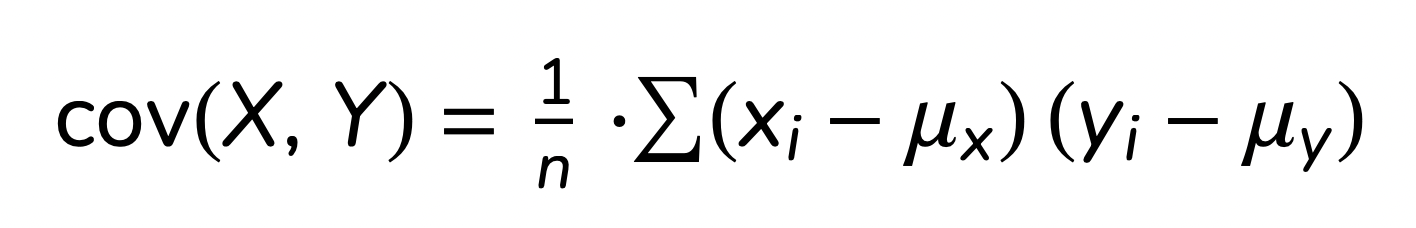
This formula helps us quantify the relationship between two variables:
If the result is positive, it suggests a positive relationship.
If it’s negative, the variables move in opposite directions.
If it’s close to zero, there’s little or no relationship.